celebbas.blogg.se

Is this in the critical region? No- because the probability that X is at least 7 is not less than 0.05 (5%), which is what we need it to be. Suppose we are given that X has a Poisson distribution and we want to carry out a hypothesis test on the mean, l, based upon a sample observation of 3. If we were to perform an upper, one-tailed test, the critical value would be t 1-, 1.6495. Note, however, that in the one-tailed test the value of the parameter can be as high as you like. For our two-tailed t-test, the critical value is t 1-/2, 1.9673, where 0.05 and 326. Then the critical region will be to the left.

Suppose we are looking for a definite decrease. If our sample value lies in this region, we reject the null hypothesis in favour of the alternative.

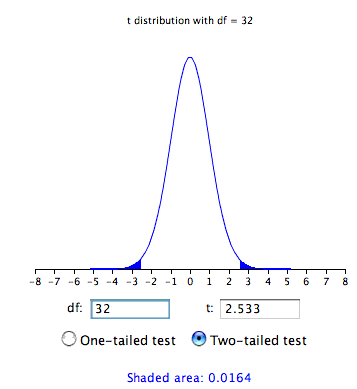
In a one-tailed test, the critical region will have just one part (the red area below).

Select if the population standard deviation,, is known or unknown. T. Since the significance level was set at 5, it is thus lower than 31. The p-value is the probability that the difference between the sample means is at least as large as what has been observed, under the assumption that the. It produces a p-value, which can be used to decide whether there is evidence of a difference between the two population means. This means that the probability that you draw a sample where both groups differ more than the groups in the example is 31. This test is known as an a two sample (or unpaired) t-test. If we perform the test at the 5% level and decide to reject the null hypothesis, we say "there is significant evidence at the 5% level to suggest the hypothesis is false". hypothesis test for a population mean given statistics calculator. Excel Function: Excel provides the function T.TEST to handle the various two-sample t-tests. In this t-test example, the p-value (2-tailed) is 0.312 or 31. For example, performing the test at a 5% level means that there is a 5% chance of wrongly rejecting H 0. We can perform the test at any level (usually 1%, 5% or 10%). A one-tailed test looks for an increase or decrease in the parameter whereas a two-tailed test looks for any change in the parameter (which can be any change- increase or decrease). There are two different types of tests that can be performed. We consider the distribution given by the null hypothesis and perform a test to determine whether or not the null hypothesis should be rejected in favour of the alternative hypothesis. The normal distribution table for left-tailed test is given below.Suppose we have a null hypothesis H 0 and an alternative hypothesis H 1. For example, you could be thinking about a population of men. The normal distribution table for right-tailed test is given below. If thats below your significance level, then you would reject your null hypothesis and it would suggest the alternative that might be that, 'Hey, maybe this mean 'is greater than zero.' On the other hand, a two-sample T test is where youre thinking about two different populations. Under the minimax design criterion, a sample size of 35 is required to test a null hypothesis of H: 0.05 versus an alternative hypothesis of H: 0.2 with a one-sided significance level of 0.028 and 85.01 power, where is the true proportion of successes. The t table for two tail probability is given below. I would like the null hypothesis to be that mu2 > mu1 and the alternative hypothesis to be mu1 < mu2. For the specific problem I am looking, I want the comparison to only be in one direction. In this case, the t critical value is 2.132. I want to perform a two-sample, one-tailed t-test to compare two means. Pick the value occurring on the intersection of mentioned row and column. Also look for the significance level α in the top row. Look for the degree of freedom in the most left column. Subtract 1 from the sample size to get the degree of freedom.ĭepending on the test, choose one tailed t distribution table or two tailed t table below. However, if you want to find critical values without using t table calculator, follow the examples given below.įind the t critical value if size of the sample is 5 and significance level is 0.05. The t distribution table (student t test distribution) consists of hundreds of values, so, it is convenient to use t table value calculator above for critical values. U is the quantile function of the normal distribution,Ĭritical value of t calculator uses all these formulas to produce exact critical values needed to accept or reject a hypothesis.Ĭalculating critical value is a tiring task because it involves looking for values into t distribution chart. Q t is the quantile function of t student distribution, one-tailed (directional) and two-tailed (non-directional) hypotheses, and the one-tailed and two-tailed probability values associated with the test.